��
��
��
��
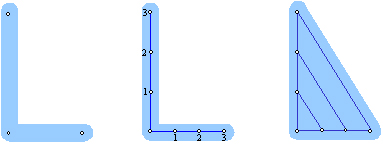
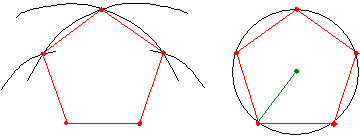
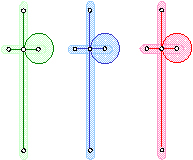
����P�R�b�������p�`�̍�}�@�@�`�A����������@�ɂ�鐳���p�`�̏������`
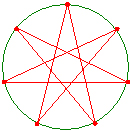
����̓R�X����K�ɂ���ď��������̂ł��B
�R�X����K�́A�q���p�̐��`���G�������ނł����A�����C�O�̏��w�Z�ɋ���x���̂��߂Ɏ����čs���A�ꕔ���ǂ��������̂ł��B
����ƁA���_�I�ɂ͐����p�`���͂��߁A���ׂĂ̐����p�`����}�\�ƂȂ����̂ł��B
���ꂩ�炨�b�����鎄�̋��ލu�`�́A�����p�`�̍�}�Ɏ���܂ł́A�R�X����K�̐����̂��b�ł��B
������O�N�قǑO�A�����̋��ލ�Ƃ̏��{����́A���w�Z�P�N���̖��ɐ��`���܊p�`�̏����������������Ǝv���܂����B
���͐��̊G���悭�`���Ă����̂ŁA�����Ɗ�Ԃ��낤�Ǝv�����̂ł��B
����ɁA���w�ɋ����������������ɂȂ�Ƃ��v�����̂ł��B
���܊p�`�̏������ׂ�ƁA�R���p�X���K�v�ł����B
���{����͔Y��ł��܂��܂����B
���w�P�N���̖��ɁA�����j�������R���p�X�͑�������A�댯���Ǝv��������ł��B
���{����́A�ŋ߂̈��S�ȃR���p�X��m��Ȃ������̂ł��B
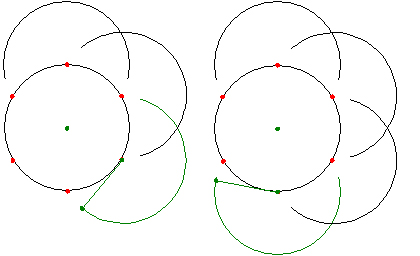
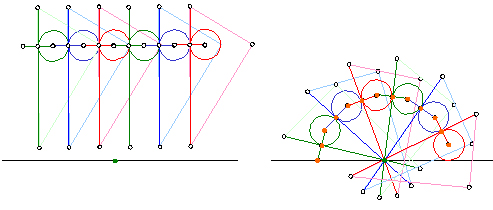
���{����́A�������^�e�ƃ��R�̒�����������ɂȂ�悤�ɂk���^�ɐ��āA���̊Ԋu�ʼn��M�̐��ʂ��R�̌��A���M�E�i����҂����j���J���܂����B
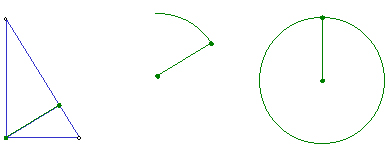
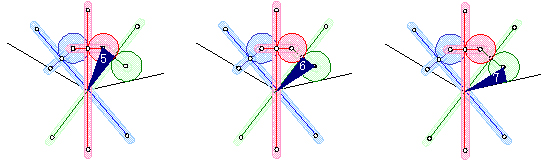
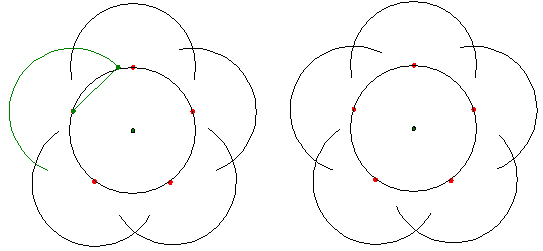
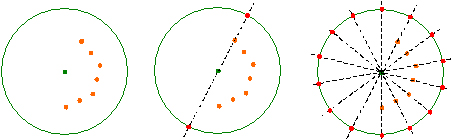
�R�X����K�̌��^�ł��B
�Q�̉��M�E�ɐc����ꂽ���M�𗼎�Ɏ����A��������]�����Ȃ���A�~�������܂��B
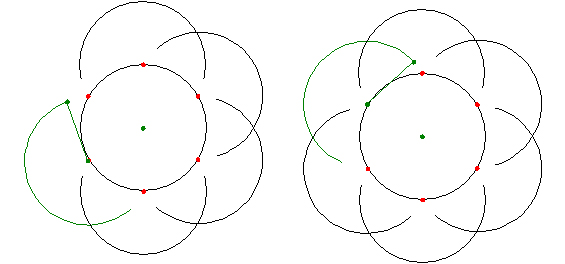
���܊p�`�́A�܂��Ԋu���Z�����M�E�Q��I��ŏ����܂��B
���̒����́A���܊p�`�̈�ӂ̒����ɑ������܂��B
���ɊԊu���������M�E�Q��I��ŏ����܂��B
���̒����́A���܊p�`�̑Ίp���̒����ɑ������܂��B

��_����Ō���Ŋ����ł��B

�R���p�X���g�킸�ɐ��`���܊p�`���������Ƃ��ł��܂����B
�����ƂĂ���̂ŁA���{����͂����Ƒ����̎q�������Ɋ��ł��炦��悤�A���ǂ������Ǝv���܂����B
�傫���̎�ނ�ԍ��ŕ\������A�ԍ��̑���ɑΉ�����_���ΐ��Ō��肵�Ă݂܂����B
���{����̖��́A���ł̓R���p�X���g����悤�ɂȂ����̂ŁA�R�X����K�͎g��Ȃ������ł��B
�R���p�X�̕����A�~�̔��a�����R�Ȓ����ɂƂ邱�Ƃ��ł��܂�����B
�ł��A�R�X����K�̌`�ł��鉩����̒��p�O�p�`�́A�R���p�X���g���Đ��܊p�`�������Ƃ��ɂ��֗��Ɏg���܂��B
�m�[�g�̍����̒��p�𗘗p���܂��B
�������Ăł������p�O�p�`�̒Z�ӂƒ��ӂɃR���p�X�����킹�Ȃ����}���Ă݂Ă��������B��قǂ̂����Ő��܊p�`���������Ƃ��ł��܂��B
���{����́A�R�X����K�𐳌܊p�`�ȊO�ɂ��Ă����܂������邩�ǂ��������Ă݂܂����B
���O�p�`�A�����`�A���Z�p�`�A�����p�`�͂��܂������܂����B
�����p�`�Ɛ���p�`�͍�}�s�\�Ƃ킩���Ă��܂����B
�������A���̐��\�p�`�́A�R���p�X�ƒ�K�ł͍�}�\�ł���̂ɁA�R�X����K�ł͂ǂ����Ă��ł��Ȃ������̂ł��B
���\�p�`�́A���܊p�`�̊O�ډ~�ƁA���̈�ӂ̓����������_�����߂���@�ō�}���܂��B
�Ƃ��낪�R�X����K�́A�R���p�X�̂悤�ɉ~�̔��a�����R�Ȓ����ɂƂ邱�Ƃ��ł��܂���B
���a�̊Ԋu�ŁA�V���ɉ��M�E��݂���K�v������̂ł��B
�R�X����K�̈�̂ǂ��ɁA���̔��a�̊Ԋu���Ƃ�����̂ł��傤���B
�����Ă��̔��a�́A��ӂ̒����ɑ��Ăǂꂭ�炢�̒����Ȃ̂ł��傤���B
���{����́A�����p�`�̊O�ډ~�̔��a�ƈ�ӂ̒����ɂ��čl���Ă݂܂����B
���O�p�`�́A���a������ӂ̒����̕��������ƒ����ł��ˁB
�����`�����l�ł��B�ł������̈Ⴂ�́A���O�p�`�����������Ȃ��Ă��܂��B
���Z�p�`�ɂȂ�ƁA���a�ƈ�ӂ̒����͓����ɂȂ��Ă��܂��B
����Ɛ��܊p�`�̊O�ډ~�̔��a�́A���܊p�`�̈�ӂ��Z������ǂ��A�����̈Ⴂ�͑傫���Ȃ��Ə��{����͎v���܂����B
���{����́A������̒��p�O�p�`�̒��p����Εӂɐ����������܂����B
��ӂ�菭���Z���Ĉ�ԏ����₷���`�́A����ȊO�Ɏv�����Ȃ���������ł��B
���̍��A���{���ǂ��w�҂̖{�ɁA"���w�͔�����"�Ə����Ă���܂����B
���{����́A�R�X����K�̐��������܊p�`�̊O�ډ~�̔��a�ł���A�V���v���łƂĂ��������Ǝv���܂����B
���w�͔������̂�����A���̒��z�͐������ƐM���܂����B
�������A���̏ؖ��͂Ȃ��Ȃ��ł��܂���ł����B
�������𗧂Ă邱�Ƃ��A���������������Ƃ��A�������\�N����������Ƃ�����܂���B
�ߏ��̍��Z���̉ƂɃP�[�L�������čs���ăm�[�g��n���A���̖��������Ă���Ȃ����Ɨ���������������������Ȃ��Ə��{����͌����Ă��܂��B
����́A���ލ�ƂɂƂ��ĂƂĂ���ȍl�����ł��B
���ލ�Ƃ̖����́A�₢�����邱�ƁA�����ł͂Ȃ����ȁH�Ƃ����A�C�f�A�������Ƃł��B
�������𗧂Ă��Ȃ��Ă��A�������������Ȃ��Ă������̂ł��B
���ꂪ�ł���l�́A���{�ɂ͂������܂��B
�����������G�Ȍv�Z�́A�ߏ��̍��Z���ɗ���ł���Ă��炢�܂��傤�B
���w�����ł������̂ł��B
�����̖��ɁA���R�Ȕ��z�Œ��ށA�₢������B
���̒��z�����������ǂ����̔��f�́A���ƂɌv�Z���Ă��炦�����̂ł��B
��낵��������A���ł�����`�����܂��B
���{����́A���ǁA���x�����s���Ȃ��玩�͂ŕ������𗧂āA�v�Z���܂����B
�C�����̔����ł́A����ȓs���̂�����������킯���Ȃ��Ǝv���Ă��܂����B
�����́A���w�͔������A�����炫���ƌv�Z�͍����ɈႢ�Ȃ��Ǝv���Ă��܂����B
�����Ă��Ɍv�Z���������Ƃ��A���{����͍����������悤�ɂȂ��āA���炭�֎q���瓮���Ȃ��Ȃ��Ă��܂��������ł��B
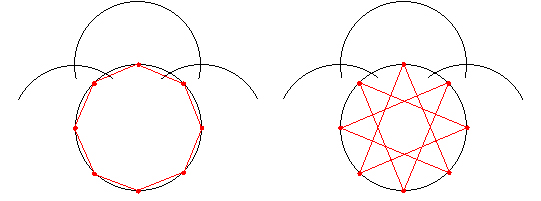
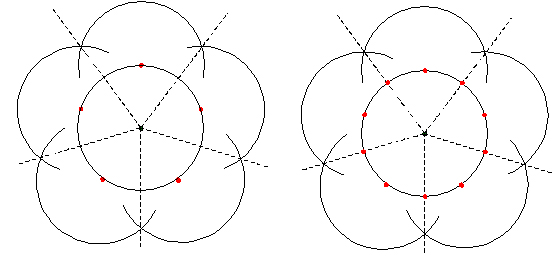
�������ăR�X����K�̊�{�`���������A���܊p�`�̍�}�@�A��Q�@���ł���悤�ɂȂ�܂����B
�����̒����a�Ƃ��ĊO�ډ~�������܂��B
�Z�ӂ̒����́A���̉~�ɓ��ڂ��鐳�܊p�`�̈�ӂł��B
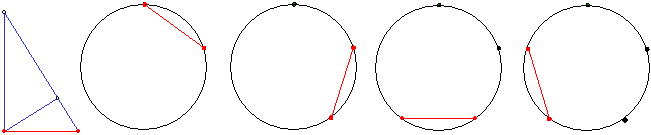
���_����Ō���Ŋ����ł��B
���̃R�X����K�̊�{�`���g���ď����鐳�܊p�`�͉���ނł��傤���H
�m���߂Ă݂܂��傤�B
�����܊p�`�̍�}�i��P�@�j
�܂����܊p�`�̈�ӂƑΊp���̒������g���ꍇ�ł��B
��ӂ�ԐF�A�Ίp����F�ŕ\���Ă��܂��B
�R�ʂ�̑傫���������邱�Ƃ��킩��܂��B
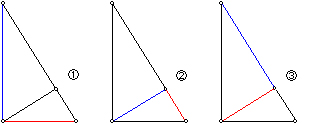
�����܊p�`�̍�}�i��Q�@�j
���ɐ��܊p�`�̈�ӂƊO�ډ~�̔��a���g���ꍇ�ł��B
��ӂ�ԐF�A�O�ډ~�̔��a��ΐF�ŕ\���Ă��܂��B
������R�ʂ�̑傫���������邱�Ƃ��킩��܂��B
��Q�@�̇@�\�Q�́A��P�@�̇@�Ɠ����傫���̐��܊p�`�������܂��B
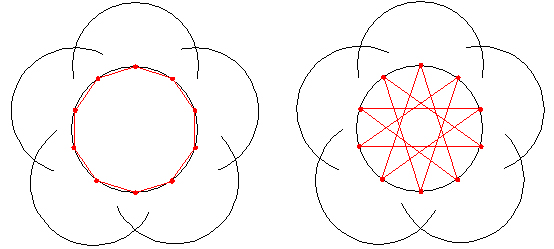
���̂��߁A�R�X����K�̊�{�`���珑�����Ƃ��ł��鐳�܊p�`�͂T��ނƂȂ�܂��B
����͎Εӂ̐����T�{�ɂ����R�X����K�ł��B
����ɂ���ď����鐳�܊p�`�̎�ނ͂T�~�T���Q�T��ނł��B
���a��N���u�̍��R����A�����C�O�֍s���O�ɋ����Ă�������̂��A���̃R�X����K�ł����B
�R�X����K�A�C���킽��B
�����Ă݂Ȃ��N���X�}�X�̐��`�������Ƃ��Ȃǂɂ������̃R�X����K���A���Ƃ�������ɊC�O�̏��w�Z�֍s���܂����B
������w���狳��x���ōs���Ă��鏬�w�Z�ł́A�q���������R���p�X�������Ă��Ȃ�����ł��B
�R���p�X���Ȃ��Ă���K�����Ő}�`�̊w�K���ł��鋳�ނƂ��āA�R�X����K����{���玝���čs�����̂ł��B
���̏����ȍ��ɂ́A�R�̖������Z��ł��āA�ނ����͑������₦�܂���ł����B
�ł����ł͕��a�ȍ��ɂȂ�A�R�̖����͒��ǂ���炵�Ă��܂��B
���̏��w�Z�ɂ��A�R�̖����̎q���������ʂ��Ă��Ă��܂��B
�Z���搶�͔w�������A�m�I�Ō��N�I�ȁA�Ί�̂₳�������̐搶�ł����B
�搶�́A�_�����Ƒz���͂��͂����ދ���d���A���w�����̂��߂̋��Ȃ̈�Ƃ��ďd�����Ă��܂����B
���̐搶���玄������ꂽ�ŏ��̂��ƁA����͗F�D���̊����q��������������悤�ɋ����邱�Ƃł����B
�߂������ɗF�D������K��c������ė���̂ŁA���̍��̍����������������Ċ��}�������Ƃ������Ƃł����B
�F�D���̊��ɂ́A���`���t���Ă��܂��B
���̎d���́A���`���܊p�`��������悤�ɋ����邱�Ƃł����B
���������p�ł��鐔�w�̎��ƂƂ��čs���̂ŁA�}�`�ւ̗�����[�߂邽�ߕ��ʗp�̌^�g�Ȃǎg�킸�A�P���P��������ō�}����Ƃ����̂��Z���搶�̍l���ł����B����ɐ��`���t���Ă��鍑���͑��ɂ���������̂ŁA�����͂�����������č��ۗ����ɂȂ������Ƃ��Z���搶�͎v�����̂ł��B
�q�������̓R���p�X�������Ă��Ȃ��̂ŁA�R���p�X���g�킸�ɐ��܊p�`���������@�Ƃ��āA���͓��{���玝���Ă����R�X����K���������Ƃɂ��܂����B
�܂����́A�R�X����K�̍����������܂����B
���̊�p�Ȏq�����l���W�߁A�����Ȕ����v���X�`�b�N�̔���ɓ���āA�\�ʂɉ������p�O�p�`�������A�D�̖͌^����Ŏg���h�����ʼn��M��ʂ����������������A�J�b�^�[�Ō`�𐮂�����@�łT�O���قǐ��삵���̂ł��B
�������ėF�D������̖K��c������Ă���܂łɁA�����̐���͊Ԃɍ����܂����B
�q��������搶�����͂����킹�āA�݂�Ȃō�����̂ł��B
�K��c���A������A���͍Z���搶���炽���ւӂ���܂����B
�������A���̓�肪����҂��Ă��܂����B
�Z���搶�́A�R�̖����̕��a�ƗF�D�̏Ƃ��Ă̐����p�`�̈Ӌ`����������A���Ўq�������ɏ��w�Z�̍Z�͂ł��鐯�`�����p�`�̏��������w�����Ă��炢�����Ƃ������̂ł��B
���͑�ύ���܂����B�����Đ����p�`�̍�}�́A���x����g���ĂR�U�O���V�̒l�ł���T�P�D�S�R�x�Ƃ����T�����g��Ȃ���Εs�\���ƍZ���搶�ɐ������܂����B
���k�����͕��x��������Ă��܂���ł����B
����������͗��R�ɂȂ�Ȃ��Ƃ����܂����B
�R���p�X���Ȃ��Ă����܊p�`�̍�}���\�ɂ����ł͂Ȃ����B
������A���x�킪�Ȃ��Ă������p�`�̍�}�͂ł���͂����ƍZ���搶�͂����̂ł��B
���́A�R���p�X�ƒ�K�̕��ʂ̎g�p�ł͍�}�ł��Ȃ��}�`����}������@�Ƃ��āA�@�B�I��}�@�Ƃ��������Ȑ��w�ł͂Ȃ����@�����邱�Ƃ�������悤�Ǝv���܂����B
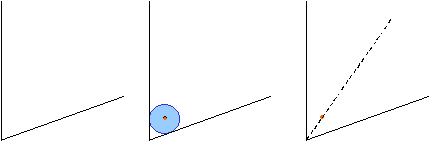
�����Ė�쌒���Y���m�́u�p�̎O�����v�Ƃ����{���Q�l�ɂ��āA�R�X����K�ɉ~��lj����Ċp�̎O������Ƃ��Ďg���Č����悤�Ǝv�����̂ł��B
�@�B�I��}�@�Ƃ��Ă��p�̎O���������E�ł��邱�Ƃ��������߂ɁE�E�E
���ꂪ�C�O�Ő��삵���R�X����K�ł��B
���{�Ŏg���Ă���R�X����K�Ƃ͏����`��ς��܂����B
�������삵���V�������ɂ́A�~���t���Ă��܂��B
����p�`����}����ړI�Ŏ����lj��������̂ł��B
���̓R�X����K�̒��́A�I���I���̎O���̂悤�ɕ����M�E�ƁA���̒������㉺�ɒ������Ə������\�����̐����̂悤�Ɍ����镔���A�����ĎO���̗��[�̈���𒆐S�Ƃ������̌��̂悤�ȉ~�̕����A���ꂪ�p�̎O�������s���������Ɛ������܂����B
�����ċ�̓I�Ȃ������������̂ł��B
����͎O�����������p�ɏƏ��������킹�A�p���Ȃ��Q�ӂ̈���ɉ~���ڂ���悤�ɂ��A�����ɉ��M�E�̂P���Q�ӂ̂�������ɏd�˂�Ƃ��A�O�̊p�ƕӂ̒����̓��������p�O�p�`���R�ł��邱�Ƃɂ��p�̎O�������s�����@�ł��B
�������A�Z���搶�͂킩��ɂ����Ƃ����܂����B
�q�������ɂ��킩��悤�ɁA���������H�v���Ȃ����Ƃ������̂ł��B
���͏\�����̐����̂悤�ȕ����ƁA���̌��̂悤�ȉ~�̕�����Ɨ������āA�����Ȕō��p�̂��̂��O��ލ��܂����B
�S���������̂͑�ςȂ̂ŁA�R�̔ǂɕ����ĂP����������̂ł��B
�������P�̔ǂɂP�̖�������Ȃ��悤�ɂ��܂����B
�܂��A�~�̕����݂̂��g���ƁA�p�����ł��邱�Ƃ������܂����B
���ɁA�\�����Ɖ~���d�˂�ƁA�p���O�����ł��邱�Ƃ������܂����B
�����Đ���p�`�̋@�B�I��}�����Ƃōs���A�Z���搶�ɂ����Ă��炢�܂����B
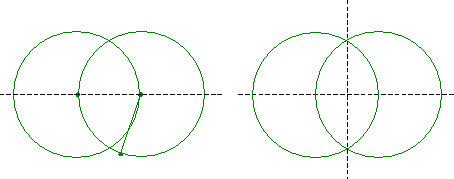
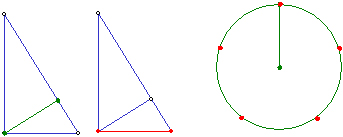
�܂��~�ɓ��ڂ��鐳�O�p�`���������@�ŁA�~�̒��S����O�̒��_�ɐ��������܂��B
�����Ă��̐����Ȃ��O�̊p���A���ꂼ��O�������čs���܂��B
�~�̒��S����A�O��������_��ʂ���������A���̐��Ɖ~�Ƃ̌�_�Ɉ��t���܂��B
���v��̈t������A���Ō���Ŋ����ł��B
�Z�ɂ̑��̊O�ł́A���l���̑��̐l���A�����̂悤�Ɍ������\��Ŏ��Ƃ����Ă��܂����B
���Ƃ��I����āA���͐E�����ōZ���搶�Ƙb�����Ă��܂����B
�Z���搶�́A��K�̌`������Ă��p�̎O���������E���Ƃ������Ƃ�[������܂����B
�ƂĂ��c�O�����ł����B
���̂Ƃ��A�Z�ɂ̊O�ɂ������̐l���E�����ɓ����Ă��܂����B
�����Ď����w�����A�����ɂ�����{�l�̂��߂ɁA�q�������͑������n�߂��A�ǂ����Ă����Ƒ吺�Ō����n�߂��̂ł��B
���ƍZ���搶�́A����Ăċ����֖߂�܂����B
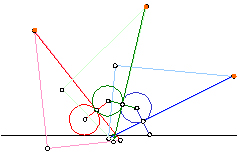
����ƁA�\�����̋��ނ��Ƃ��āA���̌��̉~�����Ƃ��āA�R�̖����̐e���i�̎q���R�l���������������������Ă���̂ł��B
���͂ł́A����q���͏��A����q���͐^���ɁA�吨�̎q���������������̉�������ł��B
��l�����͎q���������Ă�߂����悤���܂��������͂܂��܂��傫���Ȃ�A���O�̂������ƌ�������̕\��ŁA�����ɂ݂��Ă��܂��B
�q��������ł�������A��l�����̑����̂��������ɂȂ��Ă��܂��Ǝ��͎v���܂����B
���͑吺�ŁA�Â��ɂ���悤�ɁA��������߂�悤�ɂ����܂����B
�����́A�����ɐÂ��ɂȂ�܂����B
���́A�����Ă����O�l�̎q���ɁA�\�����̑����ƁA�~�̏����A���ɒu���悤�ɂ����܂����B
�q�������́A�f���ɏ\�����̑����Ɖ~�̏����d�ˍ��킹��ƁA���ɏ��̏�ɏd�˂Ēu���܂����B
����͎O�̋��ނł����B
���������̖ڂɂ́A��Ɍ������̂ł��B
���͎v�킸���̏�ɂЂ��܂����Ă��܂��܂����B
���͐S�z�����ȍZ���搶�̕\��ƁA�{���Ă����l�����̕\������܂����B
�����Ă�����肢���܂����B
"�q�������͕����u�����B
�����ĕ��a�̏ł��鐯�`�����p�`�̍�}�ɐ�������"
�݂�ȂƂĂ������Ă��܂����B
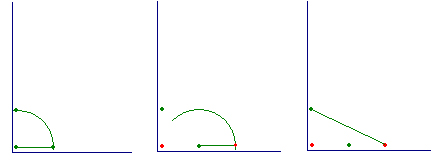
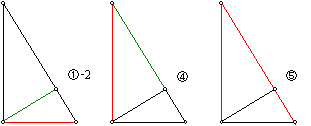
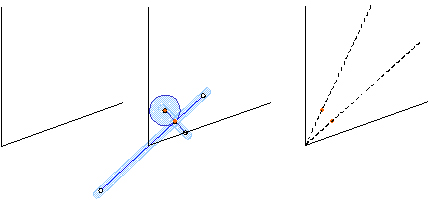
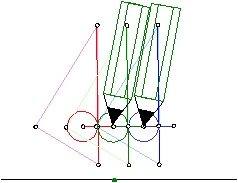
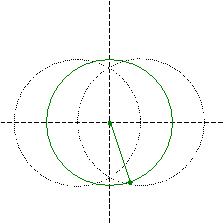
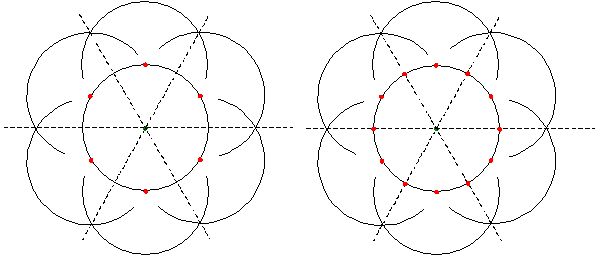
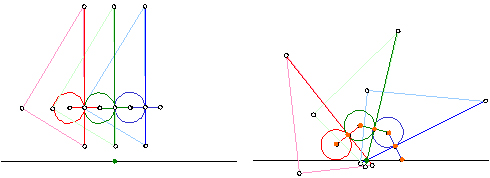
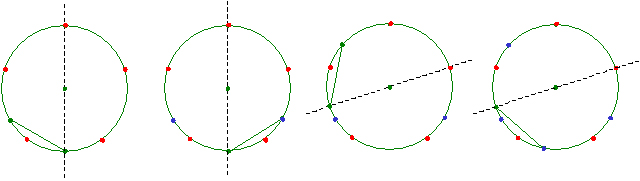
�R�X����K���R�d�ˍ��킹�邱�Ƃɂ��A�p�̎��������ł��邱�Ƃ��m���߂Ă݂܂��傤�B
�O���̂悤�ɕ����M�E�̍��E�A�~�̒��S�łȂ��E�ƁA�~�̒��S�ƂȂ��Ă���E���A���M�ȂǂŘA�����܂��B
�������������p�ɏƏ��������킹�Ȃ���A�p���Ȃ��Q�ӂ̈���ɕБ��̉~���ڂ��A�����ɔ��Α��̍E���Q�ӂ̂�������ɏd�˂�悤�ɂ��܂��B
���̂Ƃ��A�O�̊p�ƕӂ̒����̓��������p�O�p�`���V�ł��邱�Ƃɂ��A�p�̎��������ł��܂��B
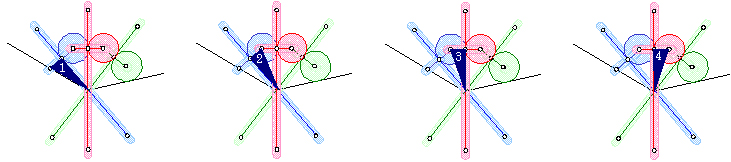
�Z���搶�͑�ϊ�сA�Z�͂ł��鐯�`�����p�`�̍�}�@���q�������Ɏw�����Ă��������ƁA���炽�߂Ă����܂����B
���͑傫�Ȗ͑��������ɍL���A�q�������ɂ悭�킩��悤�ɁA���`�����p�`�̍�}���͂��߂܂����B
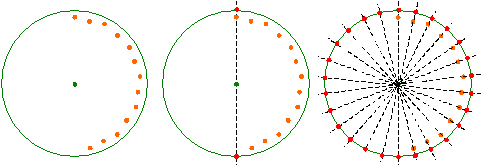
�܂����M�ŏc�ɐ��������܂��B���S�ƂȂ�ʒu�����߂Ĉ��t�����牡�ɂ��āA�R�X����K���O���p�ӂ��܂��B
��K�����M�Ȃǂ��g���ĘA�������A�O�̏Ə����𒆐S�_�ɍ��킹�Ă����܂��B
�}�̂悤�ɂ��邽�߂ɂ́A�E�̒�K�̏�ɍ��̒�K���d�ˁA����ɂ��̏�ɐ^�̒�K���d�˂ĘA��������Ƃ悢�ł��傤�B
�O�̏Ə��������S�_�ɁA�Б��̉~�ƁA���Α��̉��M�E�����ɐڂ���悤�ɂ��܂��B
����Ŏ���������_�̈ʒu�͌��܂�܂������A��K���d�Ȃ�A���̈ʒu�����Ɉ��Ƃ͂ł��܂���B
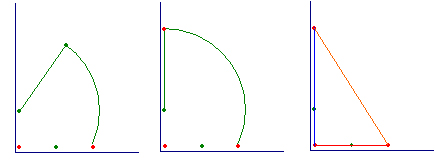
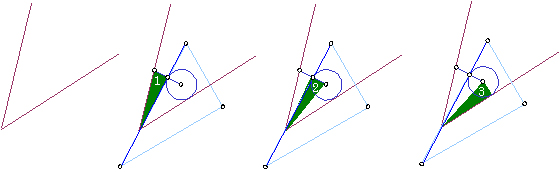
�����Œ�K�̈�ԊO���̓_�̈ʒu�ɁA��K�̈ʒu���������t���Ă����܂��B�}�ł̓I�����W�F�̎O�̈�ł��B
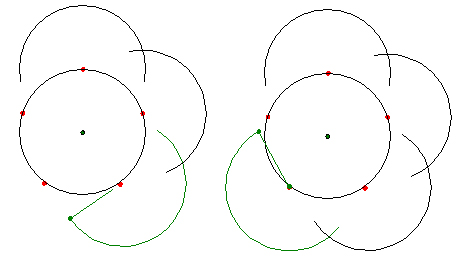
�R���̒�K���O���܂��B
�P���ڂ̒�K�̈ʒu�������_�ɒ�K�����킹�A�Ə��������S��ʂ�悤�ɂ��āA����������_�̂����R�_�Ɉ��t���܂��B
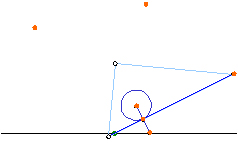
�Q���ڂ̒�K�̈ʒu�������_�ɒ�K�����킹�A�Ə��������S��ʂ�悤�ɂ��A�P���ڂŕt�����P�_�����M�E�ɍ��킹�A�V�����Q�_�Ɉ��t���܂��B
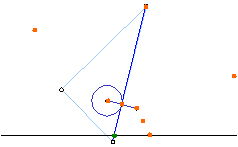
�R���ڂ̒�K�̈ʒu�������_�ɒ�K�����킹�A�Ə��������S��ʂ�悤�ɂ��A�Q���ڂŕt�����P�_�����M�E�ɍ��킹�A�V�����Q�_�Ɉ��t���܂��B
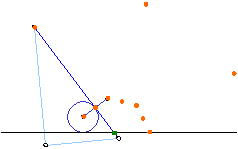
����łQ���p�P�W�O�x������������_�����܂����B���ɂ��Ă��������A�c�ɖ߂��܂��B
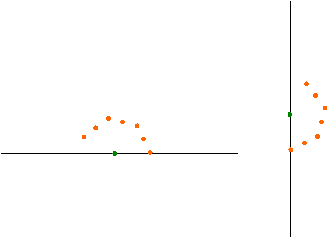
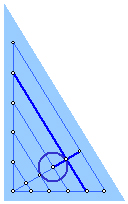
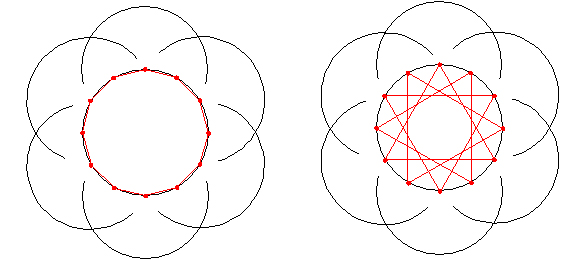
���S����D���ȑ傫���̉~�������܂��B
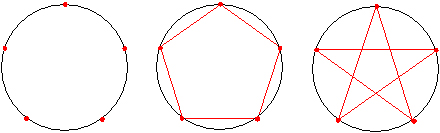
��K���������_�̂P�ƒ��S�_�ɍ��킹�A���̂Q�_��ʂ�����~�ƌ����Q�_�Ɉ��t���܂��B
�������_�̂��ׂĂɂ��ē����悤�ɍs���܂��B
�������ĕt����ꂽ�P�S�̓_�͉~���P�S�������Ă��܂��B��������ׂΐ��\�l�p�`�ł��B
�����p�`�́A���̓_���P�u���Ɍ���ł����܂��B�Ԃ��_�Ɛ��_�����݂ɗ���悤�ɔz�u���܂����B
�Ԃ��V�̓_����Ō���Ŋ����ł��B
���̒�K�͊p�̎O�����@�\�����łȂ��A�A�����������Ƃ��Ă̋@�\�������Ă����̂ł��B
�P���łR�����A�Q���łT�����A�R���łV�����A�܂肎���łQ��+�P���������_�I�ɉ\�ł��B
�A����������@�́A�����Ȑ��w�̕��@�ł͂Ȃ��A�@�B�I��}�@�̈��ł��B
���̂��߂��̒�K�́A�K�v�ɉ����Ĕ��B�������Ԑ��w�̒�K�Ƃ����Ӗ��ŁA������K�ƌĂ�ł������Ǝv���܂��B
������ɂ��鍕�p�ɁA�傫�߂̃R�X����K���������p�ӂ��܂����B
��}�ɂ��Ă̎����́A���a�䏬�w�Z�U�N���݂̂Ȃ���ɂ��肢���܂��B
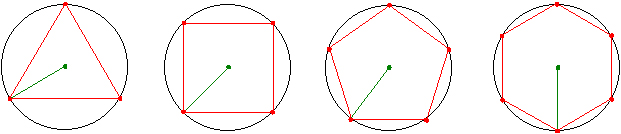
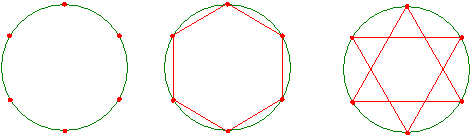
���O�p�`���琳�\�܊p�`�܂ł̍�}�@�ɂ��Ă��Љ�܂��傤�B
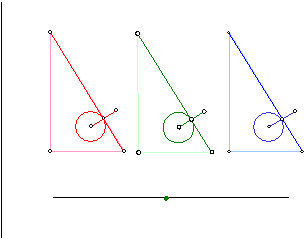
�����O�p�`�̍�}�i��P�@�j
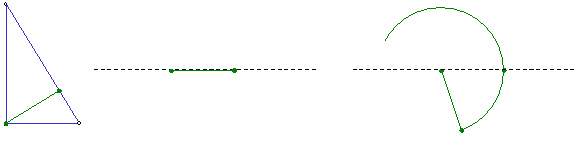
�܂��͐��R�p�`�B�O�ډ~�������Ȃ����@�ł��B


�����O�p�`�̍�}�i��Q�@�j
���ɊO�ډ~���������@�ł��B
�������`�̍�}
���ɐ����`�B
�����܊p�`�̍�}�i��P�@�j
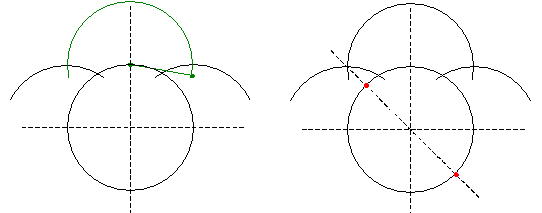
���T�p�`�̍�}��P�@�́A�R�X����K�̉�����̊W�ɂ���Z�ӂƒ��ӂ̂Q�ӂ��g���č�}������@�ł��B

�����܊p�`�̍�}�i��Q�@�j
���T�p�`�̍�}��Q�@�́A�R�X����K�̐����ƒZ�ӂ̂Q�ӂ��g���č�}������@�ł��B
���̕��@�͐��܊p�`�̊O�ډ~��������̂ŁA���\�p�`��\�܊p�`�A����\�p�`�ւƔ��W���Ă�����}�@�ł��B
��P�@�ł͊O�ډ~�������Ȃ��̂ŁA���̂悤�Ȕ��W�͂ł��܂���B



�����Z�p�`�̍�}
���U�p�`�B�������͂�����V���v���ł��ˁB
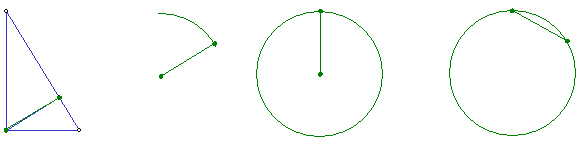
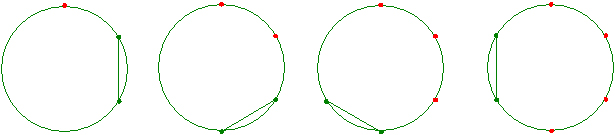
�������p�`�̍�}
���V�p�`�B�A�����������̕������R���g���܂��B







�������p�`�̍�}
���W�p�`�B����͐����`�̍�}�@�̂Ȃ��ł��łɏo���Ă��܂����B
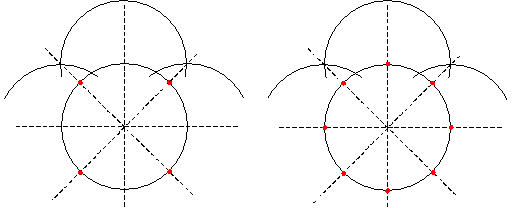
������p�`�̍�}
���X�p�`�B�~�ɓ��ڂ��鐳�O�p�`�������A�~�̒��S����O�̒��_�ֈ������������ƂɁA���ꂼ��p���O����������@�ł��B


�����\�p�`�̍�}
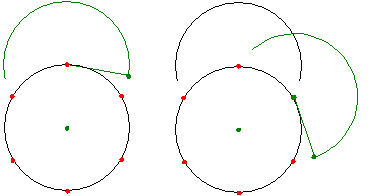
���P�O�p�`�́A���T�p�`�̊O�ډ~�ƁA���̈�ӂ̓����������_�����߂���@�ō�}���܂��B
�����\��p�`�̍�}
���P�P�p�`�B�A�����������̕������T���g���܂��B�\�����̏Ə����̒����������d�˂���������Ǝv���܂��B���p�I�ɂ͒�K�̌��݂̖�����������K�v������܂��B
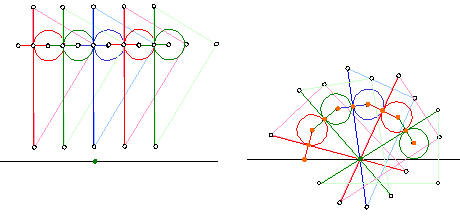
�����\��p�`�̍�}
���P�Q�p�`�́A���U�p�`�̊O�ډ~�ƁA���̈�ӂ̓����������_�����߂���@�ō�}���܂��B
�����\�O�p�`�̍�}
���P�R�p�`�B�A�����������̕������U���g���܂��B�\�����̏Ə����̒����������d�˂���������Ǝv���܂��B���p�I�ɂ͒�K�̌��݂̖�����������K�v������܂��B
�����\�l�p�`�̍�}
���P�S�p�`�B����͐��V�p�`�̍�}�@�̂Ȃ��ł��łɏo���Ă��܂����B
�����\�܊p�`�̍�}
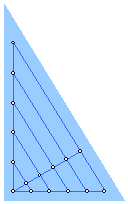
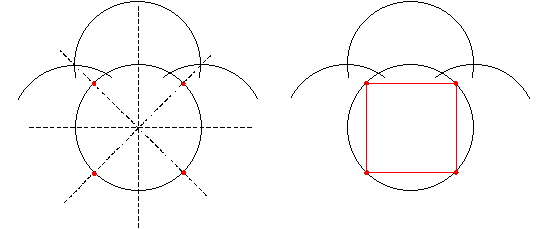
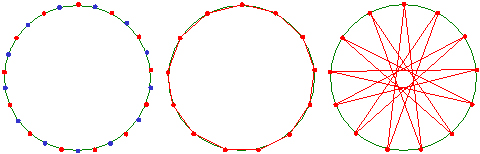
���P�T�p�`�́A���܊p�`�̊O�ډ~����{�ƂȂ�܂��B
�����Đ��܊p�`�̌܂̓_�̂����P��I�сA���̓_����Ƃ��Đ��O�p�`�̍�}��Q�@�ɂ���ĊO�ډ~�ɂQ�̓_��lj����܂��B
����ɐ��܊p�`�̌܂̓_�̂������̂S�ɂ��Ă����l�̕��@�łQ�_���lj����܂��B
���̓_�͂T�A���ꂼ��ɂ��ĂQ�_���lj������̂œ_�̐��͂R�{�̂P�T�ɂȂ��Ă��܂��B
���̂P�T�̓_�����ׂA���\�܊p�`���������܂��B
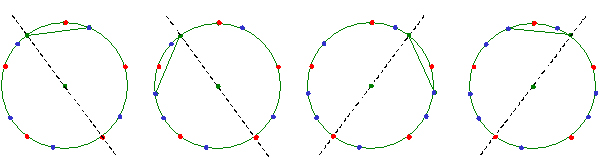
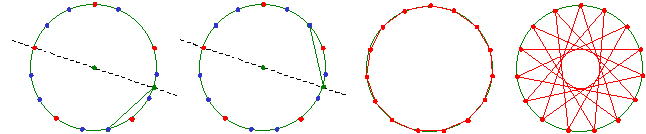
�R�X����K�̐����ߒ��ƁA���̍�}�@�ɂ��Ă��������Ă܂���܂����B
�Z���搶�́A�q�������̘_�����Ƒz���͂�{�����߂ɁA���w�Ȃǂ̕����K�v���Ƃ����Ă��܂��B
���́A�_�����Ƒz���͂ɂ��Ăǂ̂悤�ɂ��l���ł����ƁA�Z���搶�ɐu�˂Ă݂܂����B
����ƁA�Z���搶�͂����܂����B
�z���͂Ƃ́A�����͂������肽���Ƃ�����̓I�Ȗ������́B
�_�����Ƃ́A���̖������Ȃ��邽�߂ɁA���܉������ׂ����A���Ă͂Ȃ�Ȃ������l����́B
���́A��������߂��q�������̐S�̒��ɁA���̑z���͂Ƙ_���������������܂����B
������A���͌��n�ɖ߂�܂��B
���̌��ʂ��܂����������Ǝv���܂��B
�ȏ�Ŏ��̋��ލu�`���I���܂��B
���肪�Ƃ��������܂����B
����P�R�b�@�I��
�y�֘A�����@��K�ƃR���p�X���g������}�z
���܊p�`�̍�}�E�E�E�₳�������̏������@���܊p�`�Ɖ����̂k�i���ރt�@�C���@��P��j
����p�`�̍�}�E�E�E�p�̎O�������@�~�g�u�@�Ɛ���p�`�̍�}�i���ރt�@�C���@��Q��j